Các bạn đang tìm hiểu hay tìm kiếm tài liệu về cách giải các bài toán động học phải không nào? Thật sự mới đầu mình tìm hiểu về các bài toán động học này, mình cảm thấy nó quá phức tạp, khó hiểu hay không thể hiểu nổi mà các tài liệu thường viết chung chung. Nên, là một người từng tìm hiểu về các bài toán động học này để ứng dụng trong xác định vị trí tọa độ và các tính toán liên quan đến điều khiển robot. Bài viết này, mình sẽ chia sẻ cho các bạn cách giải các bài toán động học chi tiết nhất.
Mục lục
Bài toán động học thuận
Mục đích của bài toán động học thuận là xác định vị trí của khâu tác động cuối của tay máy khi biết các biến khớp của tay máy.
Các bước thực hiện bài toán động học thuận cho tay máy:
Bước 1: Xác định số khớp và số thanh nối
Bước 2: Gắn lên các thanh nối từ 0 đến n các hệ trục tọa độ
Ví dụ: Thanh nối i (i = 0 ÷ n) gắn hệ trục Oi i i i ,X ,Y , Z
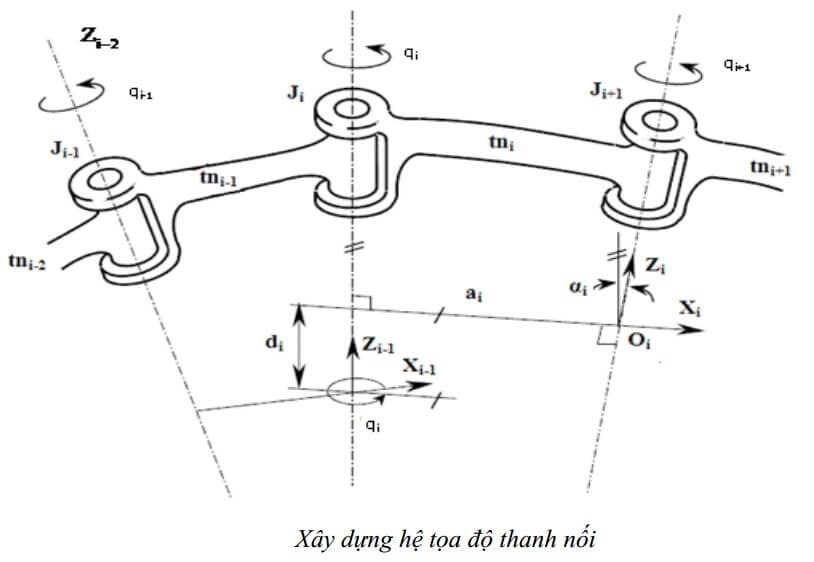
- qi: là góc quay của thanh nối thứ i,
- di: là độ lệch khâu,
- ai: là độ dài đường vuông góc chung giữa Zi-1 và Zi ,
- αi: là góc vặn của thanh nối.
Cách xác định trục Zi: là trục mà xung quanh nó khớp thứ i+1 quay hoặc dọc theo khớp (i = 1÷ n-1) tịnh tiến.
- Z0: trục mà xung quanh nó khớp 1quay,
- O0: tâm hệ trục tọa độ quy chiếu, chọn một điểm cố định trên đế Robot,
- Z1: trục mà xung quanh nó khớp 2 quay hoặc khớp tịnh tiến,
- Zn-1 : trục mà xung quanh nó khớp n quay,
- Zn: trùng phương với Zn-1
Cách xác định trục Xi: Trục X thường được đặt dọc theo pháp tuyến chung và hướng từ khớp i đến i+1. Trong trường hợp các trục khớp cắt nhau thì trục X chọn theo tích vectơ Zi-1 x Zi.
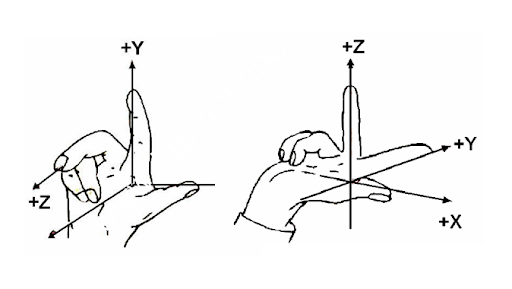
Cách xác định trục Yi: Xác định theo quy tắc bàn tay phải.
Bước 3: Xác định các biến khớp
- Khớp quay tương ứng với biến khớp quay q.
- Khớp tịnh tiến tương ứng với biến khớp tịnh tiến d.
Bước 4: Xác định quan hệ giữa hai khung tọa độ i và i-1
Hệ trục tọa độ i và hệ trục tọa độ i-1 giữa hai khâu nối tiếp nhau có quan hệ với nhau bằng phép biến đổi đồng nhất, theo trình tự sau:
- Quay xung quanh trục Zi-1 một góc θi sao cho trục Xi-1 trùng với phương của trục Xi
- Tịnh tiến dọc theo trục Zi-1 một đoạn di để gốc khung tọa độ mới trùng chân pháp
tuyến chung trục i-1 và i, (Xi-1≡ Xi), - Tịnh tiến dọc theo trục Xi-1 một đoạn ai, (Oi-1≡ Oi),
- Quay xung quanh trục Xi-1 một góc αi sao cho trục Zi-1 trùng với trục Zi.
Các phép biến đổi trên được thực hiện so với khung tọa độ hiện tại, do đó phép biến đổi tổng hợp được xác định như sau:

Bước 5: Xác định phương trình động học thuận cho tay máy.
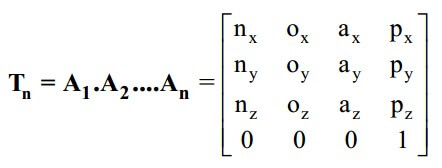
Thực hiện bài toán động học thuận như sau:
1. Xác định hệ tọa độ
Cách 1:
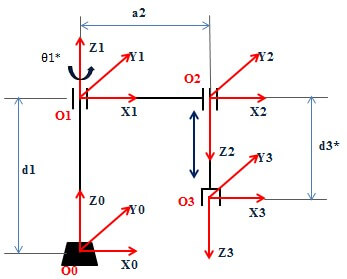
Cách 2 (chọn cách 2):
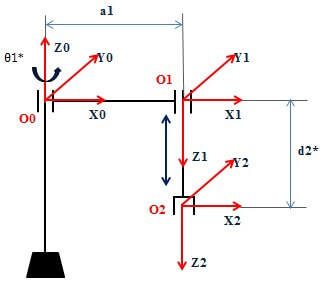
Chúng ta sẽ sử dụng cách thứ hai để đơn giản hóa các bước tính toán mà vẫn đảm bảo yêu cầu bài toán.
2. Lập bảng thông số DH
| Khâu | αi | ai | di | θi |
| 1 | 180o | a1 | 0 | θ1* |
| 2 | 0 | 0 | d2* | 0 |
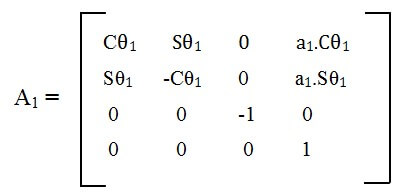
3. Xác định các ma trận Ai


Từ công thức (2.3) ta suy ra được:
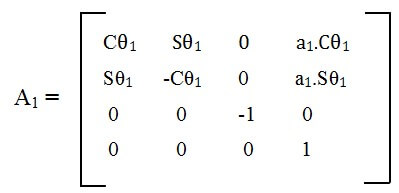

4. Tính các ma trận Ti

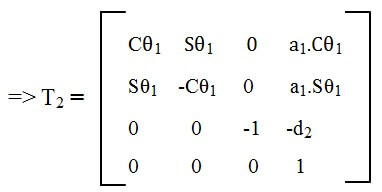
5. Thiết lập phương trình động học
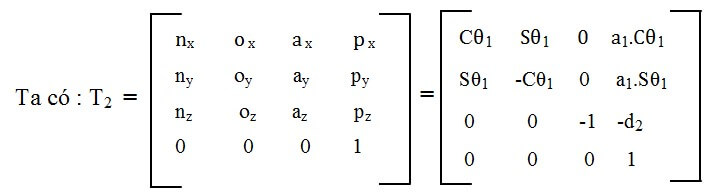
Như vậy vị trí của tay theo khung tọa độ gốc sẽ là :
- Xt = px = a1.Cθ1
- Yt = py = a1.Sθ1
- Zt = pz = -d2
Bài toán động học ngược
Mục đích của bài toán động học ngược là tìm các biến khớp của tay máy khi biết vị trí khâu tác động cuối của tay máy. Có 3 phương pháp cơ bản để xác định mô hình động học ngược của tay máy là phép đảo hướng, phép đảo vị trí và phép đảo kết hợp. Thông thường hay sử dụng phương pháp đảo kết hợp nên trong bài em đưa ra cách giải bài toán động học ngược theo phương pháp đảo kết hợp.

Giả sử:

Ta nhân cả 2 vế với ma trận nghịch đảo (A1-1) ta được: A1-1.T2 = A2
Với ma trận nghịch đảo:

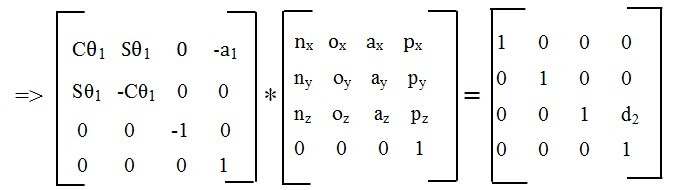
Cân bằng các thành phần cột 4 của phương trình trên ta nhận được các phương trình sau:
- Cθ1.px + Sθ1.py – a2 = 0 (2.5)
- Sθ1.px – Cθ1.py = 0 (2.6)
- –pz = d2 (2.7)
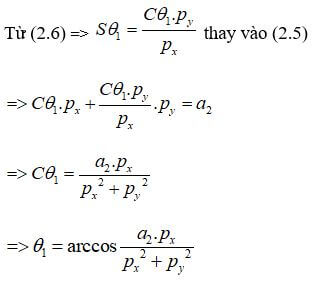
Bài toán động lực học
Thực hiện bài toán động lực học như sau:
Ta có:
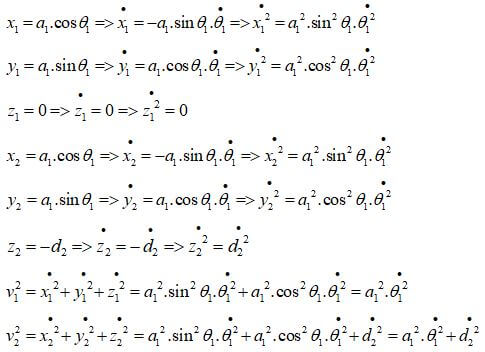
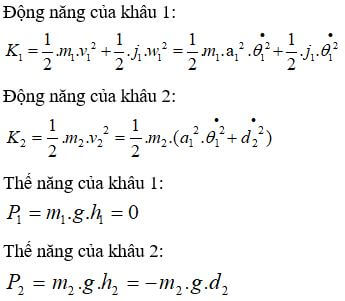
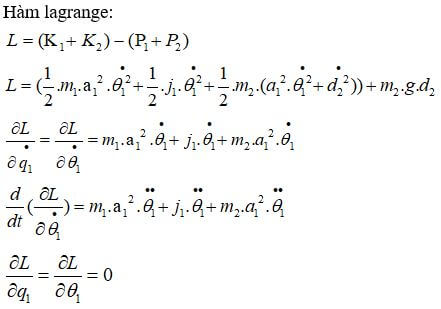
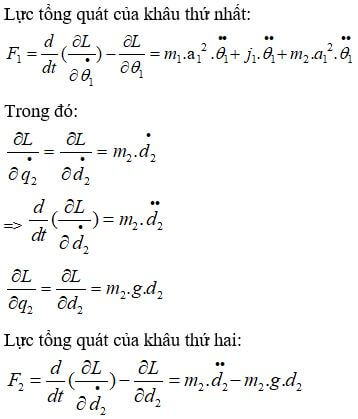
Viết dưới dạng phương trình không gian trạng thái:
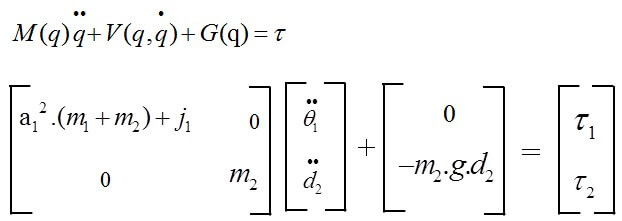
Mô phỏng bài toán động học
Chúng ta sẽ dùng phần mềm Easy-Rob để nghiên cứu thiết kế động học, các kích thước và kết cấu của robot trên máy tính để có thể chọn được phương án động học tốt nhất, đảm bảo cho robot hoàn thành các nhiệm vụ yêu cầu.
Chương trình mô phỏng chuyển động:
PROGRAMFILE erc load view my_view PTP_AX 9.4999 -10.0000 -0.0087 WAIT 1 erc load view my_view1 PTP_AX 9.4999 -10.0000 0.2793 WAIT 1 ERC LOAD TOOL AM_GRF_C ERC GRAB BODY vat1 WAIT 1 PTP_AX 9.4999 -10.0000 -0.0174 WAIT 1 erc load view my_view PTP_AX 100.9999 -10.0000 -0.0174 WAIT 1 erc load view my_view2 PTP_AX 100.9999 -10.0000 0.2880 WAIT 1 ERC LOAD TOOL AM_GRF_O ERC RELEASE BODY vat1 WAIT 1 PTP_AX 100.9999 -10.0000 -0.0262 WAIT 1 erc load view my_view PTP_AX 8.9999 -10.0000 -0.0262 WAIT 1 erc load view my_view1 PTP_AX 9.9999 -10.0000 0.2793 WAIT 1 ERC LOAD TOOL AM_GRF_C ERC GRAB BODY vat2 WAIT 1 PTP_AX 9.9999 -10.0000 -0.0262 WAIT 1 erc load view my_view PTP_AX -79.5001 -10.0000 -0.0262 WAIT 1 erc load view my_view3 PTP_AX -79.5001 -10.0000 0.2793 WAIT 1 ERC LOAD TOOL AM_GRF_O ERC RELEASE BODY vat2 WAIT 1 PTP_AX -79.5001 -10.0000 -0.0262 WAIT 1 erc load view my_view PTP_AX 8.9999 -10.0000 -0.0262 WAIT 1 ENDPROGRAMFILE
Trên đây, MESIDAS GROUP đã chia sẻ cho các bạn về khái niệm, công thức và cách bước giải các bài toán động học thuận, động học ngược và bài toán động lực học kèm theo ví dụ cụ thể và được thực nghiệm bằng mô phỏng. Chúng tôi hy vọng rằng, với những thông tin được chia sẻ phía trên sẽ giúp ích được các bạn trong quá trính tìm hiểu, nghiên cứu, học tập và làm việc liên quan tới các bài toán động học. Xin cảm ơn!

khi nào thì mình dùng phân tích động học…khi nào… Đọc thêm »
Theo như mình tìm hiểu thì: Khi nào thì dùng… Đọc thêm »
thanks